GW with fully analytic formula (general)

Here follows the most standard \(GW\) calculation with MOLGW for the ionization potential (IP) of water. \(G_0W_0\) based on BHLYP (50 %) of exact-exchange is known to be very good for IPs.

&molgw
  comment='H2O GW analytic formula'    ! an optional plain text here

  scf='BHLYP'

  basis='cc-pVTZ'
  auxil_basis='cc-pVTZ-RI'

  postscf='G0W0'

  selfenergy_state_range=0      ! will calculate just the HOMO
  frozencore='yes'              ! accurate approximation: O1s will not be included 
                                ! in the RPA/GW calculation

  natom=3
/
O      0.000000  0.000000  0.119262
H      0.000000  0.763239 -0.477047 
H      0.000000 -0.763239 -0.477047

After the SCF cycles with the BHLYP hybrid functinal, one can find the response calculation within the RPA equation:

 Prepare a polarizability spectral function with
                               Occupied states:        4
                                Virtual states:       53
                              Transition space:      212

MOLGW will then diagonalize a \(212 \times 212\) matrix. This is must often the computational bottleneck in a calculation. Memory scales as \(N^4\) and computer time as \(N^6\).

Then comes the \(GW\) quasiparticle energies and weights:

 state spin    QP energy (eV)  QP spectral weight
     5    1     -12.354761       0.915241

State 5 is the HOMO. The \(GW\) ionization potential is the negative HOMO, here 12.35 eV.

Experimental value is 12.62 eV

The discrepancy is large. Why?

GW slow convergence

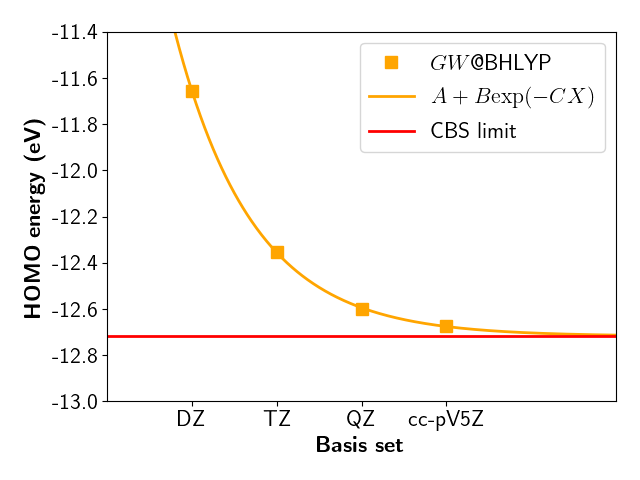
A complete basis convergnce study for GW@BHLYP would give basis convergence

with a CBS HOMO evaluated to -12.72 eV.

MOLGW automatically proposes a CBS extrapolated value based a trained linear regression:

 Extrapolation to CBS (eV)
                         <i|-\nabla^2/2|i>    Delta E_i     E_i(cc-pVTZ)      E_i(CBS)
 state    5 spin  1 :        62.271159       -0.404451      -12.354761      -12.759212

where the \(GW\) HOMO energy is -12.76 eV. So 0.04 eV away from the correct CBS, but the raw cc-pVTZ value was 0.37 eV away.

Now the experimental and \(GW\) IP agree within 0.14 eV. This is the typical accuracy of \(GW\) calculations.

GW with imaginary frequencies (HOMO LUMO gap)

If we are just interested in the HOMO LUMO region, there exists an alternative to the fully diagonalization of the RPA equation (\(N^6\) scaling).

The \(GW\) self-energy can be evaluated by numerical quadruture for imaginary frequencies and then analytically continued to real frequencies with a Padé approximant.

This is much faster (\(N^4\) scaling), however it is robust only in the HOMO-LUMO gap region and it requires more convergence parameters.

Here is a typical input file:

&molgw
  comment='H2O GW with numerical integration'

  scf='BHLYP'

  basis='cc-pVTZ'
  auxil_basis='cc-pVTZ-RI'

  postscf='G0W0_PADE'

  selfenergy_state_range=0
  frozencore='yes'

  nomega_chi_imag=16           ! frequency grid for the response function
  nomega_sigma_calc=12         ! frequency grid for sigma along the imaginary axis 
                               ! (fit of the analytic continuation)
  step_sigma_calc=0.1           
  nomega_sigma=101             ! frequency grid for sigma along the real axis

  natom=3
/
O      0.000000  0.000000  0.119262 
H      0.000000  0.763239 -0.477047 
H      0.000000 -0.763239 -0.477047

The output reports a HOMO value of -12.354 eV, which agrees within 1 meV with the previous analytic value.

 state spin    QP energy (eV)  QP spectral weight
     5    1     -12.354356       0.915308